Mr.P’s Parent Maths Problem of the Week

Hello parents,

Last week’s puzzle was based on the well-known handshake problem, but with a twist: instead of finding the number of handshakes from the number of people, we had to work backwards and figure out how many people must be in the room. The important idea here is to think about what happens as each new person arrives.

Imagine people entering the room one at a time:

•   The first person shakes no hands (no one else is there yet).
•   The second person shakes 1 hand.
•   The third person shakes 2 new hands.
•   The fourth person shakes 3 new hands.

Each new person shakes hands with everyone already there. So every time a new person arrives, the total number of handshakes increases by one more than last time.

So the running total builds like this:
0, +1, +2, +3, +4, +5, +6, +7, etc…

If you add these together step-by-step, you eventually reach 105 exactly when the 15th person arrives. So the event must have had 15 people.

Well done to everyone who had a go. 

Solutions will be published in the following week’s edition of the Barrow Hills Bulletin.

Problem 6: 13 February 2026

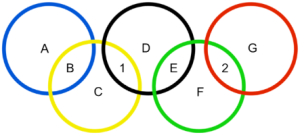
In honour of the Winter olympics, here is a nice ‘Olympic Rings’ maths problem. 

Replace the letters A-G with the digits 3-9 (the digits 1 and 2 have already been done for you) so that each Olympic Ring totals 11.